The publication provided below is concerned with showing how we can reduce the energy of particle beams injected in tokamaks while actually improving the performance. The trick is that the reduced energy, i.e., beam voltage, must be accompanied by an increase in the beam current. This allows a larger number of lower energy particles to be injected. I gave an APS Invited Talk on this topic, which was the culmination of a few years of engineering work to design and adjust the beams such that this operating mode was possible.
For the moment, DIII-D is the only facility in the world that can independently control the voltage and current of its neutral beams. Whether this is truly an advance will become apparent if other facilities invest the necessary resources to enable their beams to operate this way.
This paper appears in Physics of Plasmas as,
D. C. Pace (庞大卫), M. E. Austin, L. Bardoczi, C. S. Collins, B. Crowley, E. Davis, X. Du, J. Ferron, B. A. Grierson, W. W. Heidbrink, C. T. Holcomb, G. R. McKee, C. Pawley, C. C. Petty, M. Podestà, J. Rauch, J. T. Scoville, D. A. Spong, K. E. Thome, M. A. Van Zeeland, J. Varela, and B. Victor, Phys. Plasmas 25, 056109 (2018).
You can download the Accepted Manuscript (PDF, 4 MB).
Dynamic neutral beam current and voltage control to improve beam efficacy in tokamaks
Abstract
An engineering upgrade to the neutral beam system at the DIII-D tokamak [J.L. Luxon, Nucl. Fusion 42, 614 (2002)] enables time-dependent programming of the beam voltage and current. Initial application of this capability involves pre-programmed beam voltage and current injected into plasmas that are known to be susceptible to instabilities that are driven by energetic ( keV) beam ions. These instabilities, here all Alfvén eigenmodes (AEs), increase the transport of the beam ions beyond a classical expectation based on particle drifts and collisions. Injecting neutral beam power,
MW, at reduced voltage with increased current to reduce the drive for Alfvénic instabilities and result in improved ion confinement. In lower-confinement plasmas, this technique is applied to eliminate the presence of AEs across the mid-radius of the plasmas. Simulations of those plasmas indicate that the mode drive is decreased and the radial extent of the remaining modes is reduced compared to a higher beam voltage case. In higher-confinement plasmas, this technique reduces AE activity in the far edge and results in an interesting scenario of beam current drive improving as the beam voltage reduces from 80 kV to 65 kV.
I. INTRODUCTION
Energetic ions, sourced by beam injection, electromagnetic wave injection, or fusion reactions, serve to heat fusion plasmas and drive current that enables stable confinement. The effects of energetic ions on plasma instabilities and the mechanical issue of power loading to the reactor walls are important issues for future burning plasma devices including the ITER tokamak. [1] Present day tokamak facilities investigate energetic ion transport and various interactions with plasma waves, especially Alfvén eigenmodes (AEs). [2] A detailed overview of the state of energetic ion physics understanding is provided by Heidbrink and Sadler, [3] and a more focused overview of energetic ion interactions with AEs is provided by Breizman and Sharapov [4] [the toroidal Alfvén eigenmode (TAE) and reversed-shear Alfve ́n eigenmode (RSAE) are the modes of interest in the present work]. The rapid development of this knowledge base is leading to a fresh look on past experiments, e.g., identifying energetic ion transport by instabilities in TFTR plasmas that were not known at the time of the shots. [5]
There is an interplay between the goals of controlling energetic ion transport and improving the efficiency of neutral beam injection. One approach is to affect the instabilities without changing the energetic ion distribution, such as by injecting electromagnetic waves using an antenna as in the JET, C-Mod, and MAST tokamaks, [6] applying global error fields as in NSTX, [7] or by injecting electron cyclotron heating to alter the plasma such that mode damping is changed as in TJ-II, [8] DIII-D, [9] and ASDEX upgrade. [10] Another approach is to change the energetic ion distribution in some manner that reduces the prevalence of instabilities and then propagate some beneficial effect on the particle transport. The injection geometry of neutral beams provides an early decision point that will necessarily instill some limitation in what can be achieved with the beams. The addition of new beamlines with the increased radial tangency radius was found to stabilize some instabilities in NSTX-U, [11] while the nearly perpendicular (to the magnetic field) orientation of the W7-X neutral beam prevents it from being used for plasma startup. [12] Modifying existing neutral beams to enable time-variable current and voltage control provided for improved beam ion velocity space manipulation on DIII-D. [13]
The present work considers another way of tailoring the beam ion distribution: changing the current and voltage of the neutral beams simultaneously. For beam ions existing at velocities below the Alfvén speed of the plasma, the ion-AE energy exchange occurs at higher order resonances with a strong dependence on the ion velocity. [14] Given any particular plasma conditions, it should be possible to identify a beam voltage that minimizes the AE drive. From an engineering perspective, the power output of the beams is directly related to the voltage; therefore, any changes in voltage would also change the beam power. Independent control of neutral beam voltage and current enables a new operating mode in which power can be maintained across a range of voltages, i.e., the same power can be produced at different values of beam ion velocity. This opens up a wide range of experimental possibilities, with two examples shown here.
The results are organized as follows: Sec. II describes the DIII-D neutral beam system and engineering changes that enabled time-variable current and voltage, Sec. III describes the reduction of high frequency plasma instabilities in low-confinement (L-mode) plasmas, Sec. IV includes results of increased neutral beam current drive in high- confinement (H-mode) plasmas, and then Sec. V summarizes the conclusions.
II. NEUTRAL BEAMS AT DIII-D
A. System parameters
The DIII-D neutral beam system provides upwards of 20 MW of power for heating and driving current in the plasma. The beams inject ions across a range of energies (beam voltage), approximately described by,
kV with currents ranging across
A. Injected neutral species can be hydrogen, deuterium, or helium. Each of the eight separate beams can modulate with minimum 5ms on/off periods. The plasma control system (PCS) uses this modulation capability to enable real-time feedback of plasma stored energy and/or injected beam torque.
Figure 1 is a scaled drawing that provides the injection geometry of the eight separate beamlines (projected onto the midplane) and demonstrates their physical scale. These beams also serve many diagnostic purposes as there is no single lower-power diagnostic beam. The 150° beamline (containing the 150L and 150R neutral beams as indicated in Fig. 1) is capable of tilting vertically [15] to allow off-axis injection (it remains fixed at a single angle throughout the shot). Off-axis neutral beam injection has been well characterized, [16] and modeling of neutral beam current drive was most recently established through an international effort encompassing many different facilities. [17]

Additional flexibility is provided by the 210° beamline, which is directed in the opposite toroidal direction compared to the others. [18] This orientation allows for the injection of counter-current (counter to the plasma current) beam injection regardless of the present direction of the plasma current. While beam injection in the counter-current direction is subject to increased prompt loss levels compared to co-current injection, it remains a powerful actuator for driving rotation and heating plasmas [19] and it was a fundamental component of the discovery of the improved confinement regime known as QH-mode. [20]
B. In-shot control of beam current and voltage
A fundamental improvement in tokamak capability is achieved by keeping the injected power of a single neutral beam source fixed while its current and voltage change with time. This allows the total power to the plasma to remain constant as the physics actuators of beam ion energy (voltage) and number density (current) change. Adding the capability for the neutral beams to change their current and voltage during plasma shots was not an obvious engineering upgrade because limitations in beam divergence require the injected beam power change along with the current and voltage. This requirement is described by a parameter known as the perveance, , which is related to the beam current,
, and voltage,
, as
. The technical changes required to achieve variable perveance are discussed in other publications, [21,22] while the physics implications are provided here.
The neutral beams function by extracting ions from a filament-based plasma source, accelerating the ions through the desired voltage, passing them through a large gas chamber to neutralize a fraction of them (dependent on the accelerating voltage), and then collimating the resulting neutral stream as it enters the tokamak. The perveance indicates the extent to which space charge affects the extraction of the particle beam. Electrostatic fields arising from space charge deflect the accelerated particles away from the ideal path that expels those particles in a desired, focused, direction. In practice, there is a value of perveance for any given DIII-D neutral beam that represents the minimum space charge influence on the path of the accelerated ions. At this perveance, therefore, the ions experience the least deflection away from the desired path into the tokamak and the beams inject at the minimum divergence. The final gridded apertures of the neutral beams are 12 cm wide by 48 cm tall, so it is the vertical divergence that is of greater concern for ensuring that injected neutrals reach the plasma instead of scraping off along the walls of the beam duct or vacuum vessel port. Only vertical divergence is presented here. Typical perveance operating values are in the vicinity of . Independent control of neutral beam current and voltage necessarily allows the system to operate away from its optimum perveance and hence the phrase used to describe this operating method: Variable Beam Perveance (VBP).
If the focus of a neutral beam needs to be held fixed, i.e., a minimum divergence maintained, then any changes to either the beam current or the voltage will be limited by their ratio, . The consequence is that any intention to vary the beam current or voltage with time would also change the injected power. Two available operating modes are
- Voltage Change with Auto-perveance: the voltage is preprogrammed and the on/off modulation can be programmed separately, i.e., the voltage will follow its program regardless of whether the beam is being modulated. The Plasma Control System (PCS) [23] automatically adjusts the beam current to enforce a specific value of optimum perveance.
- Voltage and Current Change: both the beam voltage and current are pre-programmed. If the resulting perveance is too far away from optimum, then the beam will stop injecting. This stop-point is determined by a machine protection circuit that measures stray ion impacts into other parts of the neutral beam system. Experience shows that this allowable perveance range is approximately 15% from optimum.
Both operating modes provide a maximum voltage slew rate of 40 kV/s and a range of variation within a single shot of kV. The single-shot range limit is born of the way in which the power supplies set the acceleration voltage and this cannot be changed without a major hardware replacement.
C. Perveance effect on beam divergence
Considerations for implementing VBP must include an assessment of how increased beam divergence will affect device operation. Beam modeling, including divergence, [24] can be used to demonstrate that protection circuitry prevents the beams from firing in a state featuring dangerous divergence values. Aside from machine protection, it is desirable to maintain a low divergence in order to maximize the beam driven current and resultant plasma heating. In experiments, the beam divergence can be measured within the beam itself through a Doppler spectroscopy technique that makes use of an existing Multichord Divertor Spectroscopy diagnostic system. [25]

Measured divergence as a function of beam voltage is shown in Fig. 2. This shot featured the VBP mode of changing both the current and voltage in order to maintain constant power. The divergence, , is observed to vary across a range
, where
is consistent with the previously determined minimum value. Divergences above
will generally lead to a trip of the neutral beam protection circuit and are therefore not expected to be produced in experimental conditions. More detailed consideration of the effect of beam divergence in power balance calculations is provided in the Appendix.
III. REDUCED ALFVÉN EIGENMODE ACTIVITY IN L-MODE PLASMAS
There is a physics motivation to test VBP in easily reproducible plasmas that are conducive to modeling and simulation. Such an experiment is designed around a base of an oval-shaped plasma that is physically limited against the center post with plasma parameters of toroidal magnetic field T, plasma current
MA, and vertical elongation
. This regime, utilizing injected neutral beam power levels between 1 and 10 MW and some variation in elongation, is the basis for many DIII-D investigations into Alfvén eigenmode stability and resulting beam ion transport. These include beam ion losses due to core-localized reversed-shear AEs, [26] AE stability for predictions of ITER behavior, [27] AE drive from beam ions that complete only a single poloidal circuit, [28,29] and the critical gradient nature of beam ion transport. [30]
It is emphasized that this experiment focuses on understanding the physics behind the wave-ion interactions that allow injected beam ions to drive Alfvénic instabilities. As such, this experiment included a secondary effort to perform engineering checks on the VBP implementation. Some of the instability results may have been similarly produced with constant voltage injection; however, varying the injected beam parameters in these L-modes helped to prepare the system for the H-mode experiments discussed later.
The experiment consists of reproducing an L-mode plasma with approximately 2.5 MW of injected beam power with minimal beam modulation and the largest possible variation in beam voltage. Radial profiles of the resulting plasma parameters are shown in Fig. 3. These profiles are representative across multiple shots and are used in all AE simulations. From the profiles, it is possible to classify this plasma as low density [Fig. 3(a)] with a significant beam ion pressure contribution [Fig. 3(b)], and a reversed-shear high q-profile [Fig. 3(c)] that is conducive to producing AEs.

The full neutral beam heating for these plasmas involves two neutral beams injecting continuously during the first second of the shot (taking advantage of the high-q period when plasma current is still moving inward from the edge). These beams (150L and 150R, see Fig. 1) are directed on-axis and execute a voltage change from 56 kV to 69 kV over approximately 500ms. Two other neutral beams inject widely spaced pulses of 10 ms duration for diagnostic purposes.
Figure 4 shows the beam voltages and the total injected beam power for a shot that begins with lower voltage (169128, red trace) and a comparison shot beginning with higher voltage injection (169129, black trace). Total beam power is well matched across this time period. A brief, but large, increase in total beam power is present over ms when two neutral beams inject at 80 kV for diagnostic purposes.


Differences in the AE spectra produced by these plasmas are indicated by the spectrograms in Fig. 5. These spectrograms represent a global overview of the density fluctuations in the plasma because the cross-power is calculated between vertical and horizontal interferometer chords, [31] which are measurements of line-integrated density and its fluctuation. Both shots show fluctuations in the frequency range of 50 – 150kHz, with the upward frequency sweeping RSAEs and the nearly fixed frequency TAEs indicated by annotations. The same amplitude color scale is used in each panel, indicating that the initially higher voltage shot of Fig. 5(a) features larger TAE amplitude and longer-lived RSAEs compared to the initially lower voltage shot of Fig. 5(b).
After 700 ms, the AE activity nearly disappears from both shots, which is caused by the continued decrease in the q-profile as the plasma current penetrates. This is only coincidental with the cross-over of the beam voltages as shown in Fig. 4. In similar shots with greater neutral beam power it is possible to continue to drive AEs beyond the 1000 ms mark [32]. As shown in Sec. IV, AEs are regularly produced in shots featuring moderate neutral beam heating and q-profiles with minimum values () just above 2.

While the apparent number density and amplitude of AEs is reduced in the lower voltage shot, the observed spatial extent of the modes is also different between the two plasmas. Figure 6 is a cross-power of electron temperature fluctuations incorporating multiple points from the electron cyclotron emission diagnostic system [33]. All of these measurements are acquired within a range of normalized minor radius, , given by
, and therefore represent the presence of instabilities in the mid-radius of the plasma. The higher beam voltage case shown in Fig. 6(a) features well defined fluctuations associated with TAEs. By comparison, the lower voltage shot of Fig. 6(b) provides only hints of equivalent fluctuations.
Purposely affecting the spatial extent of instabilities can be a useful tool for controlling transport levels in a tokamak plasma. Experiments [34] and simulations [35] indicate that the resulting energetic ion transport due to Alfvénic instabilities is largely determined according to the amount of spatial overlap of the AEs. Even if the amplitude of the AE spectrum was largely unaffected by reduced beam voltage, an improvement in beam ion confinement may still result from the reduced overlap of the remaining modes.
This plasma scenario is simulated with the FAR3D [36] code to examine the theoretical changes in AE stability and eigenstructure as a function of the variable beam perveance. FAR3D solves the reduced, non-linear, resistive MHD equations including linear wave-ion resonances. It identifies the most unstable mode, i.e., the mode with the largest growth rate, and includes the beam ion population as a high temperature Maxwellian distribution. The input plasma profiles for these simulations are shown in Fig. 3.

Figure 7 shows the calculated growth rate for the and
modes as a function of beam ion energy. Here, the beam ion energy is recorded as the velocity of the beam ions compared to the Alfvén velocity,
, where
is the effective temperature of the beams ions and
is set by the plasma parameters and remains constant across simulations. The eigensolver of FAR3D searches for modes in the frequency range of
kHz. Of these identified modes, the range of frequency does not change significantly across the scan of beam ion energy. Modes with negative growth rates are stable and indicated by black circles in the figure. Unstable modes feature positive growth rates and are represented by red circles. While a trend in the growth rates is not apparent, there appears to be a threshold effect resulting in the complete lack of unstable modes for
. The growth rate decrease is the result of reduced resonant drive (again, plasma terms such as the mode damping are constant across simulations).
Beam ion velocity effects on the spatial structure of the modes are shown in Fig. 8. These two panels display the calculated eigenstructure (potential fluctuation amplitude) for the case over approximately a factor of two in beam ion velocity. Figure 8(a) shows a radially extended mode structure at
, and Fig. 8(b) shows a considerably narrower mode structure at
. This result is consistent with the observed reduction (nearly complete reduction) of AE activity in the mid-radius region as presented in Fig. 6.
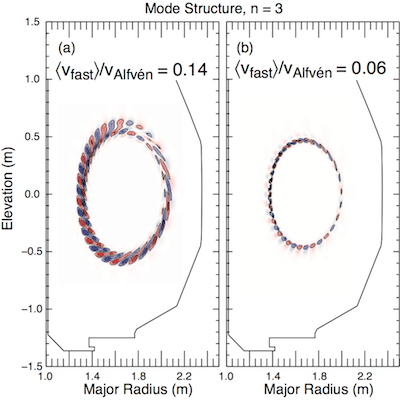
and (b)
[NOTE: this should say 0.06]
IV. INCREASED BEAM CURRENT DRIVE IN HIGH qmin SCENARIO
The steady state tokamak scenario known as “high ” features
and has been extensively investigated at DIII-D [37] and EAST. [38] The experiment begins with the same plasma characteristics of Holcomb et al., [37]
T,
MA,
, and line-integrated electron densities, $latex n_e$, in the range of
m-3, and then implements variable beam perveance to compare beam efficacy at similar powers but different voltages. The total injected beam power is approximately 7 MW. The 150 neutral beam is injected at its maximum off-axis tilt angle and Alfvén eigenmode stability in the presence of off-axis beams is well known. [39]
In contrast to the plasmas discussed in Sec. III, the shots presented here feature the same neutral beam injection characteristics through ms. Three neutral beams were available for VBP in these shots (there are seven beams capable of VBP presently), with two of those beams injecting off-axis. The plasma stored energy is controlled in the feedback mode by the PCS and the variable perveance beams operate at 70 kV. Over
ms (annotated in later figures as the Beam IV Change period), the so-called lower voltage shots execute VBP programs that decrease voltage to 65 kV or lower while increasing the beam current to reach 7 MW of total injected power. The higher voltage shots execute a pre-programmed waveform that takes the beams to 80 kV while decreasing the beam current.

Temporal waveforms for two shots are shown in Fig. 9. The line-integrated electron density averaged m-3 in the higher voltage shot, compared to the value of
m-3 in the comparison shot. Differences in plasma behavior related to this density inequality are accounted for by the TRANSP [40] analysis and modeling code. Note that the greater density of the 80 kV shot should improve beam ion confinement by facilitating slowing down of the injected particles. The slowing down time in the core of the 80 kV shot is approximately 90 ms, which is 18% shorter than the 110 ms slowing down time of the 65 kV shot. Figure 9(a) shows that both shots feature normalized
values at 2 or greater. The total injected neutral beam power is shown in Fig. 9(b), and it differs by 0.3 MW (4%) in these shots. Figure 9(c) shows the voltage evolution of the 150 L neutral beam.
Modeling of the beam ion transport is accomplished using the TRANSP code. TRANSP features an operating mode in which it varies an ad hoc beam ion diffusivity, , as needed to match the measured neutron rate from the plasma. This provides a good indication of the level of beam ion transport because the largest contributor to deuterium-deuterium (DD) fusion is beam-plasma fusion (peak electron temperatures are below 4keV). This concept is generally applied to beam heated tokamak plasmas and was most recently detailed in a study from MAST. [41] A TRANSP calculation in which
represents the classically expected level of beam ion transport, i.e., transport resulting from collisions, charge exchange, and particle drifts. The classical calculations are denoted “No Modes” as they represent the expected behavior if there were no plasma instabilities affecting the beam ions. The use of the OMFIT [42] codebase in executing these calculations greatly improves the flexibility and organization as multiple shots and different modeling setups are implemented.

Figure 10 provides an example of the effect on the neutron rate. Figure 10(a) compares the measured neutron rate (black trace) with the classical expectation (
, No Modes, dashed blue trace) and the result of the TRANSP-identified optimum
value (With Modes, red trace). The classically expected neutron rate is 50% higher than the measured rate. TRANSP is fully capable, however, of identifying the value of
necessary to match the measured rate. This time-varying value of
is provided in Fig. 10(b) with the appropriate With Modes label.
A comparison of the values deduced from the neutron rates is given in Fig. 11 for the lower and higher beam voltage shots. For
ms, the values are equal, and then they both plummet during the initial beam voltage change. It is a common, and unexplained, observation that measures of plasma performance transiently improve during the beginning of a VBP period. It remains to be determined whether this is an authentic result of the changing plasma heating, e.g., possibly due to increased rotational shear as the radial profile of beam torque changes, or some more mundane issue related to modeling of the initial evolution. Regardless, the
values reach different stable values across the stationary period of
ms. Within that time period, the beam ion diffusivity of the higher beam voltage shot is approximately twice that of the lower beam voltage shot.

An example of the sensitivity of the neutron rate to the beam ion confinement is also provided in Fig. 11. The brief spikes occurring at and 3300 ms result from 10 ms wide pulses of the 30 L neutral beam at 81 kV. The temporary increase in beam power at high voltage serves to drive fluctuations that cause transport of the greater beam ion population. Of interest to note is that the change in
from this high energy beam pulse reduces with time for the lower beam voltage shot. While the
ms pulse of 30 L increases beam ion diffusivity from
cm2/s to
cm2/s (53% increase), the second pulse at
ms only increases it from
cm2/s to
cm2/s (25% increase). This is qualitatively consistent with the idea that the lower beam voltage shot has a smaller population of high energy beam ions because they are sourced only by the 30L pulse. By comparison, shot 170803 features multiple beams near 80kV injection and that provides a much larger population to be affected by the additional instability drive of the 30L pulse. The 3000 ms pulse of 30L in shot 170799 produces nearly the same change in
as shot 170803 because the slowing down of the 70 kV beam ions has not been completed, i.e., both shots feature a more similar beam ion distribution at 3000 ms.

The fluctuation spectra between these higher and lower beam voltage shots demonstrate one obvious difference: an 80 kHz mode appears only in the higher beam voltage plasma. Figure 12 is a spectrogram of density fluctuations measured with the beam emission spectroscopy diagnostic system (BES). [43] This cross-spectrum includes BES positions at normalized minor radii, , of
and
. Figure 12(a) annotates the spectrogram to indicate the TAE frequency range of
kHz and the 80 kHz mode that is unique to the higher beam voltage shot. The immediate, and brief, reduction in fluctuations across
kHz following the appearance of an edge localized mode (ELM) is indicated in Fig. 12(b). In addition to the presence of the 80 kHz mode, the higher beam voltage shot features larger amplitude TAEs that reappear along with the recovery of the 80 kHz mode after each ELM.

Spatial profiles of the fluctuations are shown in Fig. 13. The TAEs are once again indicated in Fig. 13(a), where the 80 kHz mode is labeled as the Edge Mode. These spectrograms are produced using BES across a spatial array over at
ms in both shots. A striking difference is that the higher beam voltage shot of Fig. 13(a) shows much greater fluctuation power in the frequency range
kHz compared to the lower beam voltage shot. There are indications of coupling between the 80 kHz mode and the TAEs near 200 kHz in Fig. 13(a), and the radial extent of that triplet of modes is suitable for increasing the transport of beam ions. Reduced fluctuation amplitudes and radial extent in the lower beam voltage shot of Fig. 13(b) are important for achieving improved beam ion confinement in this scenario featuring off-axis beam injection and a large population of beam ions seeded within the mid-radius region.

The realized improvement in neutral beam application comes in the form of increased beam current drive for the lower beam voltage plasma. Figure 14 displays the calculated beam current drive density for the two high shots of this section and an additional shot that injected beams at 50 kV or lower through the stationary period. While the 50 kV shot utilized the same stored energy feedback as the other shots of interest, the voltage range limitation of the beams required that it begin injection (
ms) at 55 kV and it is not an exact reproduction of the conditions of the other shots. For the sake of this current drive example, however, it demonstrates an interesting feature of reduced voltage beams.
The neutral beam driven current density plots are separated into two results. Figure 14(a) shows the current drive density for these three cases using the TRANSP modeling of classical beam ion transport, . This display therefore accounts for any expected differences in the beam current drive due to small differences in plasma parameters, e.g., beam current drive should be increased at lower plasma density as experienced in the lower beam voltage shot. Under the classical expectation, the beam current drive of the higher and lower beam voltage shots should be equivalent. Classically, the slightly better beam current drive in the 65 kV shot arises from the 30% lower plasma density compared to the higher voltage shot. At the same densities, the current drive would reduce as the beam voltage reduced. Setting the beam voltage to 50 kV results in a large reduction of the current drive entirely due to the reduced velocity and increased edge deposition of those beams.
Accounting for the beam transport effect of plasma instabilities leads to a very different outcome. Figure 14(b) shows that the lower beam voltage case at 65 kV actually produces a better beam current drive scenario than the 80 kV case. The entire panel of Fig. 14(b) is one-half scale compared to Fig. 14(a), so this result is not an indication of the complete eradication of instability-related beam efficacy reductions. Seeing as how the lowest beam voltage case at 50 kV has closed some of the gap to compete with the 80 kV case, however, does confirm that the transport effect of instabilities is sensitive to the velocity and orbit topology of beam ions. This result is also consistent with experiments and modeling that showed that instabilities can account for large reductions of neutral beam current drive in NSTX. [44] This phenomenon is well suited to further investigation by simulations that incorporate a full beam ion velocity space distribution. Neutral beam current drive is strongly dependent on the orbit topology of the beam ions and is best examined by considering transport within velocity space. One promising method for approaching this topic is to use the Kick Model [45] integrated into TRANSP to apply AE-induced beam ion transport to more finely resolved areas of velocity space. This has been done for some DIII-D experiments and provided more detailed computations of the resulting beam current drive. [32]
It is also clarifying to consider this result in the context of beam ion transport due to microinstabilities, i.e., broadband turbulence. While initial theoretical and experimental work claimed to show that beam ion current drive was noticeably reduced by the presence of microturbulence, later work from ASDEX Upgrade [46] and DIII-D [47] demonstrated that this was not an actual effect. The concept of microturbulence-induced energetic ion transport is well demonstrated to have an inverse energy dependence in basic plasma devices. [48,49] Such a dependence suggests that reduced neutral beam voltage is even more likely to suffer enhanced diffusion compared to higher beam voltage plasmas. In that regard, then, the present results further demonstrate the lack of microturbulence-induced energetic ion transport in the parameter space of present tokamaks.
V. CONCLUSIONS AND DISCUSSION
Dynamic neutral beam voltage and current control can allow the injected beam ion population to evolve along with plasma characteristics in order to minimize the drive of Alfvén eigenmodes and other instabilities that enhance beam ion trans- port beyond the classically expected (i.e., considering particle drifts and collisions) level. The trivial achievement of this capability might see the injected beam power change along with the voltage, but independent beam voltage and current control allows a wider range of beam voltages to produce the same amount of total power. Producing the same power at different values of beam current and voltage increases the beam divergence above the minimal value originally designed into the system. This increase reaches up to approximately in the DIII-D case, which is acceptable in terms of machine protection and allows 20 kV beam changes in a shot with a slewing rate of 40kV/s across a range of beam current changes. The process of changing beam current and voltage outside of the optimum ratio (perveance, given by
) is called Variable Beam Perveance (VBP).
Variable beam perveance has been applied to L-mode plasmas in DIII-D by comparing the same 2 MW of injected beam power at different values of beam voltage and current. Importantly, this is accomplished without using power modulation techniques, and a stationary plasma condition is obtained. With beam injection at 80 kV, radially extended toroidal Alfvén eigenmodes (TAEs) are produced, but this group of modes is not present in a similar shot taken with 65 kV beam injection. Simulations that include ion-AE resonant interactions show that the AE drive reduces as the beam voltage is reduced and that the modes excited at 65 kV are localized closer to the plasma core.
The VBP technique is then applied to a high steady state scenario plasma. At 7 MW of injected beam power and off-axis injection from two of the beams, a comparison is made between 80 kV and 65 kV injection. The 80 kV case produces considerable mode activity in the far edge of the plasma and this includes greater edge TAE activity compared to the 65kV case. Modeling shows that the neutral beam driven current is greater at 65 kV injection than at 80 kV, in contrast to classical expectations.
A conceptual summary of these results is that using reduced beam injection voltage to reduce plasma instabilities is only viable if implemented as VBP; otherwise, the reduced beam voltages always require a similar reduction in the total power injected. By increasing the beam current during a voltage reduction, it is possible to maintain the same power level produced in a higher voltage shot, i.e., VBP allows for the injection of a greater number of lower energy neutrals. Next steps for this concept should involve determinations of the ion-AE resonance space in ITER configurations to determine whether a VBP-like technique might be useful for affecting the instability spectrum excited by ITER’s 1 MeV neutral beam injection or actively damping AEs generated by 3.5 MeV fusion born alphas. For present machines, modeling and simulation can be used to identify new applications of VBP by identifying regimes in which increased slew rates or greater voltage and current excursions can respond to plasma evolution in real-time.
ACKNOWLEDGMENTS
This material was based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, using the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Award Nos. DE-FC02-04ER54698, DE-FG03-97ER54415, DE-AC52-07NA27344, DE-AC02-09CH11466, DE-FG02- 94ER54235, and DE-FG02-08ER54999. DIII-D data shown in this paper can be obtained in digital format by following the links at https://fusion.gat.com/global/D3D_DMP.
Experimental time was allotted to this effort as part of the Torkil Jensen Award (TJA). The TJA, consisting of one run day, is given in recognition for outstanding proposals for innovative experiments using the capabilities of the DIII-D National Fusion Facility.
The research presented in this paper combined engineering developments and a demanding operational plan for the application of variable beam perveance to different plasmas. Many members of the DIII-D team contributed their time to aid in the success of this project. We are grateful to the DIII-D Operations Group for their limitless enthusiasm for designing and implementing changes to the substantial neutral beam system. We also wish to thank A. R. Briesemeister for loaning the use of her spectrometer diagnostic for the measurement of beam divergence, C. Lasnier and M. Makowski for running their infrared camera system across the multiple days of this experiment, and M. Gorelenkova for explaining TRANSP’s treatment of neutral beam parameters.
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
APPENDIX: BEAM DIVERGENCE IN TRANSP
The creation of time-dependent neutral beam current and voltage was masterfully handled by the TRANSP team. While the temporal evolution of beam voltage and power was already possible in TRANSP, the beam divergence remains a scalar value that is set in the namelist (TRANSP setup file). This means that the beam divergence is modeled at its minimum value throughout the calculation. While Fig. 2 demonstrates that the change in vertical divergence is small, the resulting changes in beam deposition and orbit topology are not themselves obviously small, i.e., the beam ion velocity space distribution may change in meaningful ways. To investigate this technical issue, a series of TRANSP calculations were run at different values of beam divergence for all beams that enacted VBP behavior on a shot of interest.

Figure 15 shows results of neutral beam ion density and driven current density at two different values of vertical beam divergence. The divergence of the individual beams varies little, so the reported standard value is 1.3° . The standard value is compared to an artificial doubling that produces a divergence of 2.5° . The measured excursion of divergence never reaches a value as high as 2.5°, so this modeling is intended to provide a worst-case scenario for any inaccuracies resulting from the static divergence in TRANSP. In Fig. 15(a), it can be seen that the radial profile of beam ion density is within the uncertainty ribbon for these two divergence values. Figure 15(b) shows the same result for the radial profile of beam driven current density. The trend is certainly that the beam driven current is reduced as the divergence increases, which is expected since a more poorly focused beam must be sending more neutrals into the surrounding physical structures and seeding ions in the far edge of the plasma where current drive efficiency is minimal.
Figure 15(b) shows the temporal evolution of the beam driven current density beginning with the initial VBP period at t = 2500 ms. Even during the relatively short VBP period, the effect of doubling the beam divergence is mostly within the uncertainty of the calculation. In consideration of future experiments using VBP and the possibility that time-variable beam divergence will grossly affect power balance calculations, a request for implementing beam divergence as a time variable input has been submitted. [50]
1 S. D. Pinches, I. T. Chapman, P. W. Lauber, H. J. C. Oliver, S. E. Sharapov, K. Shinohara, and K. Tani, Phys. Plasmas 22, 021807 (2015).
2 W. W. Heidbrink, Phys. Plasmas 15, 055501 (2008).
3 W. Heidbrink and G. Sadler, Nucl. Fusion 34, 535 (1994).
4 B. N. Breizman and S. E. Sharapov, Plasma Phys. Controlled Fusion 53, 054001 (2011).
5 E. D. Fredrickson, M. G. Bell, R. V. Budny, D. S. Darrow, and R. White, Phys. Plasmas 22, 032501 (2015).
6 A. Fasoli, D. Testa, T. Panis, A. Klein, J. A. Snipes, J. Sears, M. Gryaznevich, R. Martin, S. D. Pinches, and J.-E. Contributors, Plasma Phys. Controlled Fusion 52, 075015 (2010).
7 A. Bortolon, W. W. Heidbrink, G. J. Kramer, J.-K. Park, E. D. Fredrickson, J. D. Lore, and M. Podesta`, Phys. Rev. Lett. 110, 265008 (2013).
8 K. Nagaoka, T. Ido, E. Ascasıbar, T. Estrada, S. Yamamoto, A. Melnikov, A. Cappa, C. Hidalgo, M. Pedrosa, B. van Milligen, I. Pastor, M. Liniers, M. Ochando, A. Shimizu, L. Eliseev, S. Ohshima, K. Mukai, Y. Takeiri, and the TJ-II Team, Nucl. Fusion 53, 072004 (2013).
9 M. V. Zeeland, W. Heidbrink, S. Sharapov, D. Spong, A. Cappa, X. Chen, C. Collins, M. G.-M. noz, N. Gorelenkov, G. Kramer, P. Lauber, Z. Lin, and C. Petty, Nucl. Fusion 56, 112007 (2016).
10 S. E. Sharapov, M. Garcia-Munoz, M. A. V. Zeeland, B. Bobkov, I. G. J. Classen, J. Ferreira, A. Figueiredo, M. Fitzgerald, J. Galdon-Quiroga, D. Gallart, B. Geiger, J. Gonzalez-Martin, T. Johnson, P. Lauber, M. Mantsinen, F. Nabais, V. Nikolaeva, M. Rodriguez-Ramos, L. Sanchis- Sanchez, P. A. Schneider, A. Snicker, P. Vallejos, the AUG Team, and the EUROfusion MST1 Team, Plasma Phys. Controlled Fusion 60, 014026 (2018).
11 E. D. Fredrickson, E. V. Belova, D. J. Battaglia, R. E. Bell, N. A. Crocker, D. S. Darrow, A. Diallo, S. P. Gerhardt, N. N. Gorelenkov, B. P. LeBlanc, M. Podesta`, and N.-U. Team, Phys. Rev. Lett. 118, 265001 (2017).
12 D. Gradic, A. Dinklage, R. Brakel, P. McNeely, M. Osakabe, N. Rust, R. Wolf, the W7-X Team, and the LHD Experimental Group, Nucl. Fusion 55, 033002 (2015).
13 D. C. Pace, C. Collins, B. Crowley, B. Grierson, W. Heidbrink, C. Pawley, J. Rauch, J. Scoville, M. V. Zeeland, Y. Zhu, and The DIII-D Team, Nucl. Fusion 57, 014001 (2017).
14 R. Nazikian, N. N. Gorelenkov, B. Alper, H. L. Berk, D. Borba, R. V. Budny, G. Y. Fu, W. W. Heidbrink, G. J. Kramer, M. A. Makowski, S. D. Pinches, S. E. Sharapov, W. M. Solomon, E. J. Strait, R. B. White, M. A. Van Zeeland, and JET-EFDA Contributors, Phys. Plasmas 15, 056107 (2008).
15 C. Murphy, M. Abrahim, P. Anderson, H. Chiu, H. Grunloh, M. Hansink, K. Holtrop, R.-M. Hong, A. Kellman, D. Kellman, P. Mauzey, S. Noraky, C. Pawley, J. Rauch, J. Scoville, M. Van Zeeland, H. Yip, R. Wood, M. Murakami, J. Park, and W. Heidbrink, in 2011 IEEE/NPSS 24th Symposium on Fusion Engineering (SOFE) (2011), pp. 1–6.
16 W. Heidbrink, M. V. Zeeland, B. Grierson, C. Muscatello, J. Park, C. Petty, R. Prater, and Y. Zhu, Nucl. Fusion 52, 094005 (2012).
17 T. Suzuki, R. Akers, D. Gates, S. Gunter, W. Heidbrink, J. Hobirk, T. Luce, M. Murakami, J. Park, M. Turnyanskiy, and the ITPA, “Integrated Operation Scenarios’ group members and experts,” Nucl. Fusion 51, 083020 (2011).
18 J. Scoville, Fusion Sci. Technol. 52, 398 (2007).
19 P. Helander, R. J. Akers, and L.-G. Eriksson, Phys. Plasmas 12, 112503 (2005).
20 K. H. Burrell, W. P. West, E. J. Doyle, M. E. Austin, T. A. Casper, P. Gohil, C. M. Greenfield, R. J. Groebner, A. W. Hyatt, R. J. Jayakumar, D. H. Kaplan, L. L. Lao, A. W. Leonard, M. A. Makowski, G. R. McKee, T. H. Osborne, P. B. Snyder, W. M. Solomon, D. M. Thomas, T. L. Rhodes, E. J. Strait, M. R. Wade, G. Wang, and L. Zeng, Phys. Plasmas 12, 056121 (2005).
21 C. Pawley, B. Crowley, D. Pace, J. Rauch, J. Scoville, D. Kellman, and A. Kellman, Fusion Eng. Des. 123, 453 (2017).
22 J. Rauch, D. C. Pace, B. Crowley, R. D. Johnson, D. H. Kellman, C. J. Pawley, and J. T. Scoville, Fusion Sci. Technol. 72, 500 (2017).
23 B. G. Penaflor, J. R. Ferron, A. W. Hyatt, M. L. Walker, R. D. Johnson, D. A. Piglowski, E. Kolemen, A. S. Welander, and M. J. Lanctot, in 2013 IEEE 25th Symposium on Fusion Engineering (SOFE) (2013), pp. 1–4.
24 B. Crowley, J. Rauch, and J. Scoville, Fusion Eng. Des. 96-97, 443 (2015), proceedings of the 28th Symposium On Fusion Technology (SOFT-28).
25 N. H. Brooks, A. Howald, K. Klepper, and P. West, Rev. Sci. Instrum. 63, 5167 (1992).
26 D. C. Pace, R. Fisher, M. G. Munoz, W. Heidbrink, and M. Van Zeeland, Plasma Phys. Controlled Fusion 53, 062001 (2011).
27 M. V. Zeeland, N. Gorelenkov, W. Heidbrink, G. Kramer, D. Spong, M. Austin, R. Fisher, M. G.-M. noz, M. Gorelenkova, N. Luhmann, M. Murakami, R. Nazikian, D. Pace, J. Park, B. Tobias, and R. White, Nucl. Fusion 52, 094023 (2012).
28 X. Chen, M. E. Austin, R. K. Fisher, W. W. Heidbrink, G. J. Kramer, R. Nazikian, D. C. Pace, C. C. Petty, and M. A. Van Zeeland, Phys. Rev. Lett. 110, 065004 (2013).
29 W. W. Heidbrink, E. A. D. Persico, M. E. Austin, X. Chen, D. C. Pace, and M. A. Van Zeeland, Phys. Plasmas 23, 022503 (2016).
30 C. S. Collins, W. W. Heidbrink, M. E. Austin, G. J. Kramer, D. C. Pace, C. C. Petty, L. Stagner, M. A. Van Zeeland, R. B. White, Y. B. Zhu, and DIII-D Team, Phys. Rev. Lett. 116, 095001 (2016).
31 M. A. Van Zeeland, R. L. Boivin, T. N. Carlstrom, T. Deterly, and D. K. Finkenthal, Rev. Sci. Instrum. 77, 10F325 (2006).
32 C. Collins, W. Heidbrink, M. Podesta, R. White, G. Kramer, D. Pace, C. Petty, L. Stagner, M. V. Zeeland, Y. Zhu, and The DIII-D Team, Nucl. Fusion 57, 086005 (2017).
33 M. E. Austin and J. Lohr, Rev. Sci. Instrum. 74, 1457 (2003).
34 M. Garcıa-Munoz, N. Hicks, R. van Voornveld, I. G. J. Classen, R. Bilato, V. Bobkov, M. Bruedgam, H.-U. Fahrbach, V. Igochine, S. Jaemsae, M. Maraschek, K. Sassenberg, and ASDEX Upgrade Team, Phys. Rev. Lett. 104, 185002 (2010).
35 Y. Todo, M. V. Zeeland, A. Bierwage, and W. Heidbrink, Nucl. Fusion 54, 104012 (2014).
36 J. Varela, D. Spong, and L. Garcia, Nucl. Fusion 57, 046018 (2017).
37 C. T. Holcomb, W. W. Heidbrink, J. R. Ferron, M. A. Van Zeeland, A. M. Garofalo, W. M. Solomon, X. Gong, D. Mueller, B. Grierson, E. M. Bass, C. Collins, J. M. Park, K. Kim, T. C. Luce, F. Turco, D. C. Pace, Q. Ren, and M. Podesta, Phys. Plasmas 22, 055904 (2015).
38 B. Wan, J. Li, H. Guo, Y. Liang, G. Xu, and X. G, for the EAST Team, and I. Collaborators, Nucl. Fusion 53, 104006 (2013).
39 W. Heidbrink, M. V. Zeeland, M. Austin, E. Bass, K. Ghantous, N. Gorelenkov, B. Grierson, D. Spong, and B. Tobias, Nucl. Fusion 53, 093006 (2013).
40 see http://transpweb.pppl.gov/development-1 for A collection of docu- ments detailing TRANSP calculations and abilities, 2017.
41 I. Klimek, M. Cecconello, M. Gorelenkova, D. Keeling, A. Meakins, O. Jones, R. Akers, I. Lupelli, M. Turnyanskiy, G. Ericsson, and the MAST Team, Nucl. Fusion 55, 023003 (2015).
42 O. Meneghini, S. Smith, L. Lao, O. Izacard, Q. Ren, J. Park, J. Candy, Z. Wang, C. Luna, V. Izzo, B. Grierson, P. Snyder, C. Holland, J. Penna, G. Lu, P. Raum, A. McCubbin, D. Orlov, E. Belli, N. Ferraro, R. Prater, T. Osborne, A. Turnbull, and G. Staebler, Nucl. Fusion 55, 083008 (2015).
43 G. McKee, R. Ashley, R. Durst, R. Fonck, M. Jakubowski, K. Tritz, K. Burrell, C. Greenfield, and J. Robinson, Rev. Sci. Instrum. 70, 913 (1999).
44 M. Podesta, M. Gorelenkova, D. Darrow, E. Fredrickson, S. Gerhardt, and R. White, Nucl. Fusion 55, 053018 (2015).
45 M. Podesta, M. Gorelenkova, N. N. Gorelenkov, and R. B. White, Plasma Phys. Controlled Fusion 59, 095008 (2017).
46 B. Geiger, M. Weiland, A. Mlynek, M. Reich, A. Bock, M. Dunne, R. Dux, E. Fable, R. Fischer, M. Garcia-Munoz, J. Hobirk, C. Hopf, S. Nielsen, T. Odstrcil, C. Rapson, D. Rittich, F. Ryter, M. Salewski, P. A. Schneider, G. Tardini, and M. Willensdorfer, Plasma Phys. Controlled Fusion 57, 014018 (2015).
47 D. C. Pace, M. E. Austin, E. M. Bass, R. V. Budny, W. W. Heidbrink, J. C. Hillesheim, C. T. Holcomb, M. Gorelenkova, B. A. Grierson, D. C. McCune, G. R. McKee, C. M. Muscatello, J. M. Park, C. C. Petty, T. L. Rhodes, G. M. Staebler, T. Suzuki, M. A. Van Zeeland, R. E. Waltz, G. Wang, A. E. White, Z. Yan, X. Yuan, and Y. B. Zhu, Phys. Plasmas 20, 056108 (2013).
48 S. Zhou, W. W. Heidbrink, H. Boehmer, R. McWilliams, T. Carter, S. Vincena, S. K. P. Tripathi, P. Popovich, B. Friedman, and F. Jenko, Phys. Plasmas 17, 092103 (2010).
49 K. Gustafson, P. Ricci, A. Bovet, I. Furno, and A. Fasoli, Phys. Plasmas 19, 062306 (2012).
50 TRANSP User Group, Meeting held at the American Physical Society – Division of Plasma Physics Conference, Milwaukee, WI, 23-27 October 2017.
Leave a Reply